Advertisements
Advertisements
प्रश्न
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
उत्तर
i . Perimeter of shaded region = Length of the arc APB + Length of the arc ARC + Length of the arc BSD + Length of the arc CQD
`=1/2xx2pi"r"_1 + 1/2xx2pi"r"_2 + 1/2xx2pi"r"_4`
`=1/2xx2pi(7/2) + 1/2xx2pi(7)+1/2xx2pi(7/2)`
`=2pi(7/2)+2pi(7)`
`=2pi(7/2+7)`
`=2xx22/7xx21/2`
= 66 cm
ii . Area of shaded region = Area of the arc ARC + Area of the arc BSD - (Area of the arc APB + Area of the arc CQD)
`=1/2xxpi("r"_1)^2+1/2xxpi("r")^2 - [1/2xxpi("r"_3)^2 + 1/2xxpi("r"_4)^2]`
`=1/2xxpi(7)^2+1/2xxpi(7)^2 - [1/2xxpi(7/2)^2+1/2xxpi(7/2)^2]`
`= pi(7)^2 - pi(7/2)^2`
`=pi(49 - 49/4)`
`=22/7xx147/4`
= 115.5 cm2
APPEARS IN
संबंधित प्रश्न
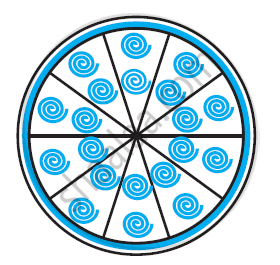
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
