Advertisements
Advertisements
प्रश्न
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
उत्तर
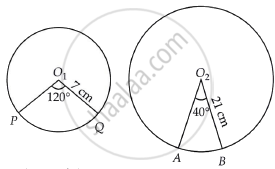
Let the lengths of the corresponding arcs be l1 and l2.
Given that, radius of sector PO1QP = 7 cm
And radius of sector AO2BA = 21 cm
Central angle of the sector PO1QP (θ1) = 120°
And central angle of the sector AO2BA (θ2) = 40°
∴ Area of the sector with central angle O1
= `(pi"r"^2)/360^circ xx θ_1`
= `(pi(7)^2)/360^circ xx 120^circ`
= `22/7 xx (7 xx 7)/360^circ xx 120^circ`
= `(22 xx 7)/3`
= `154/3 "cm"^2`
And area of the sector with central angle O2
= `(pi"r"^2)/360^circ xx θ_2`
= `(pi(21)^2)/360^circ xx 40^circ`
= `22/7 xx (21 xx 21)/360^circ xx 40^circ`
= `(22 xx 3 xx 21)/9`
= 22 × 7
= 154 cm2
Now, corresponding arc length of the sector PO1QP
= `θ_1/360^circ xx 2pi"r"`
= `120^circ/360^circ xx 2 xx 22/7 xx 7`
= `44/3 "cm"`
And corresponding arc length of the sector AO2BA
= `θ_2/360^circ xx 2pi"r"`
= `40^circ/360^circ xx 2 xx 22/7 xx 21`
= `44/3 "cm"`
Hence, we observe that arc lengths of two sectors of two different circles may be equal but their area need not be equal.
APPEARS IN
संबंधित प्रश्न
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
