Advertisements
Advertisements
प्रश्न
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
उत्तर
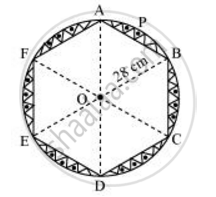
It can be observed that these designs are segments of the circle.
Consider segment APB. Chord AB is a side of the hexagon. Each chord will substitute `(360º)/6` = 60º at the centre of the circle.
In ΔOAB,
∠OAB = ∠OBA (As OA = OB)
∠AOB = 60°
∠OAB + ∠OBA + ∠AOB = 180°
2∠OAB = 180° − 60° = 120°
∠OAB = 60°
Therefore, ΔOAB is an equilateral triangle.
Area of ΔOAB = `sqrt3/4 xx ("side")^2`
`=sqrt3/4 xx (28)^2 `
` = 196sqrt3`
` = 196 xx 1.7 `
= 333.2 cm2
Area of sector OAPB = `60^@/360^@ xx pir^2`
`= 1/6xx 22/7xx28xx28`
`= 1232/3 cm^2`
Area of segment APB = Area of sector OAPB − Area of ΔOAB
`=(1232/3 - 333.2) cm^2`
Therefore, the number of designs = `6xx(1232/3 - 333.2) cm^2`
`= (2464 - 1999.2) cm^2`
= 464.8 cm2
Cost of making 1 cm2 designs = Rs 0.35
Cost of making 464.76 cm2 designs = 464.8 × 0.35 = Rs 162.68
Therefore, the cost of making such designs is Rs. 162.68.
APPEARS IN
संबंधित प्रश्न
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

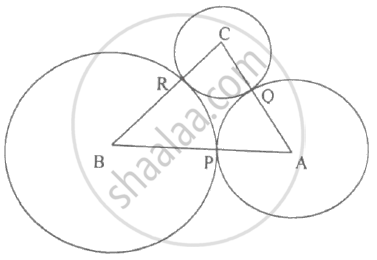
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
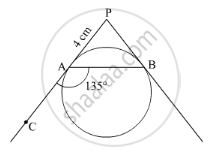
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
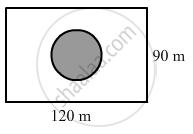
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.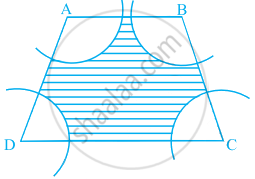
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
