Advertisements
Advertisements
Question
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use
Solution
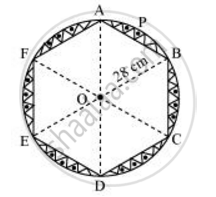
It can be observed that these designs are segments of the circle.
Consider segment APB. Chord AB is a side of the hexagon. Each chord will substitute
In ΔOAB,
∠OAB = ∠OBA (As OA = OB)
∠AOB = 60°
∠OAB + ∠OBA + ∠AOB = 180°
2∠OAB = 180° − 60° = 120°
∠OAB = 60°
Therefore, ΔOAB is an equilateral triangle.
Area of ΔOAB =
= 333.2 cm2
Area of sector OAPB =
Area of segment APB = Area of sector OAPB − Area of ΔOAB
Therefore, the number of designs =
= 464.8 cm2
Cost of making 1 cm2 designs = Rs 0.35
Cost of making 464.76 cm2 designs = 464.8 × 0.35 = Rs 162.68
Therefore, the cost of making such designs is Rs. 162.68.
APPEARS IN
RELATED QUESTIONS
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use
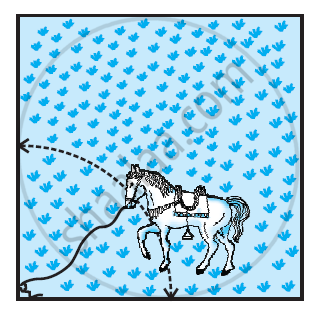
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
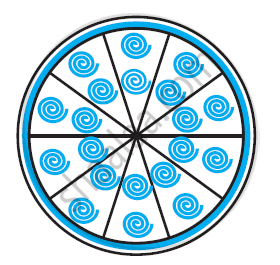
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π =
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =
(ii) A = 25r – r2
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. (

In the given figure, if A is the centre of the circle.

The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
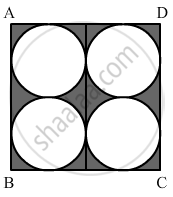
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
