Advertisements
Advertisements
Question
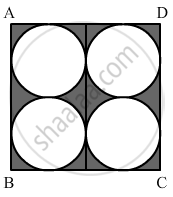
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
Solution
Area of the square = Side2 = 142 = 196 sq.cm
Area of the circles `= 4xxpixx3.5xx3.5=154 "sq". "cm"`
Area of the shaded region = Area of the square -- Area of four circles
= 196 -154
= 42 cm2
APPEARS IN
RELATED QUESTIONS
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
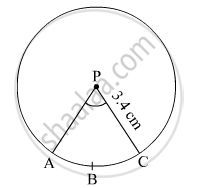
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
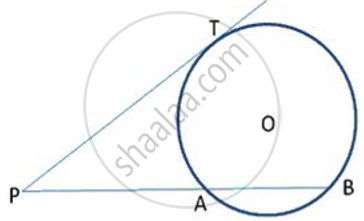
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
