Advertisements
Advertisements
Question
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
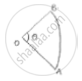
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
Solution
(i) Radius of circle = ‘r’ cm
Angle subtended at centre = 𝜃
Perimeter = OA + OB + (AB arc)
= r + r +`theta/360^@× 2pir = 2r + 2r [(pitheta)/360^@]`
But perimeter given as 50
`50 = 2r [1 +(pitheta)/360^@]`
⇒`(pitheta)/360^@=50/(2r)− 1`
⇒ 𝜃 =`360^@/pi[25/r− 1]` …..(i)
(ii) Area of sector =`theta/360^@× pir^2`
=`((360^@/pi)(25/r−1))/360^@× pir^2`
=`25/r× r^2 − r^2`
= 25r – r2
⇒ A = 25r – r2 …..(ii)
APPEARS IN
RELATED QUESTIONS
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
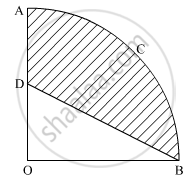
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Find the area of the unshaded region shown in the given figure.