Question

The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.

Options

• 24 cm²

• 249 cm²

• 288 cm²

• `196 sqrt2  "cm"^2`

Answer 1

The area of the largest square that can be inscribed in a circle of radius 12 cm is 288 cm².

Explanation:

Radius of the circle = 12 cm

`therefore` Diameter of circle = 24 cm.

`therefore` Diagonal of squre = 24 cm

Let the side of square = x cm.

`"x"^2 + "x"^2 = (24)^2` (Pythagoras theoram)

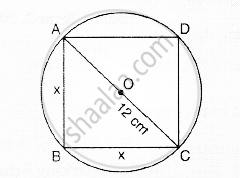
or, `2 "x"^2 = 24 xx 24`

or, `"x"^2 = (24 xx 24)/2 = 288`

Area of squre = `"x"^2 = 288  "cm"^2`