Advertisements
Advertisements
प्रश्न
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
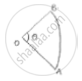
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
उत्तर
(i) Radius of circle = ‘r’ cm
Angle subtended at centre = 𝜃
Perimeter = OA + OB + (AB arc)
= r + r +`theta/360^@× 2pir = 2r + 2r [(pitheta)/360^@]`
But perimeter given as 50
`50 = 2r [1 +(pitheta)/360^@]`
⇒`(pitheta)/360^@=50/(2r)− 1`
⇒ 𝜃 =`360^@/pi[25/r− 1]` …..(i)
(ii) Area of sector =`theta/360^@× pir^2`
=`((360^@/pi)(25/r−1))/360^@× pir^2`
=`25/r× r^2 − r^2`
= 25r – r2
⇒ A = 25r – r2 …..(ii)
APPEARS IN
संबंधित प्रश्न
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
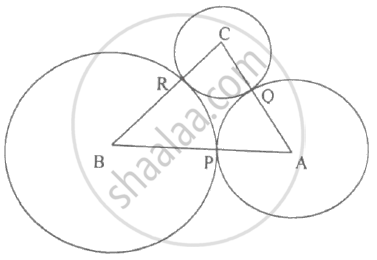
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
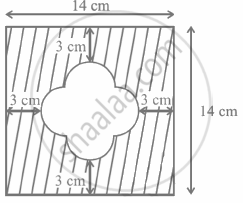
Find the area of the unshaded region shown in the given figure.