Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
рдЙрддреНрддрд░
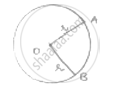
Radius = OA = OB (From fig) = r
= 5.7 m
Perimeter = 27.2 m
Let angle subtended at centre = ЁЭЬГ
Perimeter =`(theta/360^@× 2pir) `+ ЁЭСВЁЭР┤ + ЁЭСВЁЭР╡
=`theta/360^@`× 2(5.7) × ЁЭЬЛ + 2(5.7)
=`(2pi(5.7)theta)/360^@`+ 11.4
`=( pi(5.7)theta)/180^@`+ 11.4 = 27.2
=`(pi(5.7)theta)/180^@`= 15.8
ЁЭР┤ЁЭСЯЁЭСТЁЭСО ЁЭСЬЁЭСУ ЁЭСаЁЭСТЁЭСРЁЭСбЁЭСЬЁЭСЯ =`theta/360^@× pir^2`
`=158.8/360×22/7`× 5.7 × 5.7
= 45.048 cm2
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
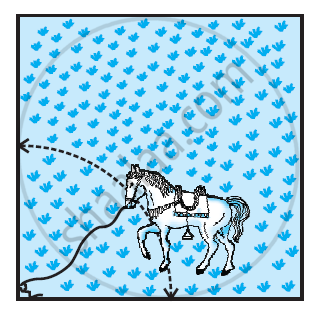
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
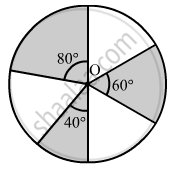
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
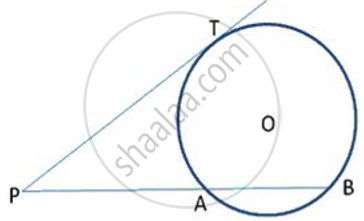
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.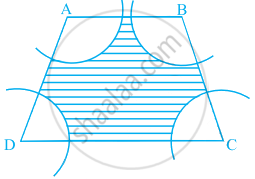
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
