Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
рдЙрддреНрддрд░
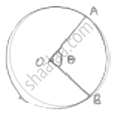
ЁЭЬГ = angle subtended at centre
Radius (r) = 5.6m = OA ± OB
Perimeter of sector = 27.2 m
(AB arc length) + OA + OB = 27.2
⇒`(theta/360^@× 2pir)` + 5.6 + 5.6 ± 27.2
⇒`(5.6 pitheta)/180^@`+ 11.2 = 27.2
⇒ `5.6 ×22/7`× ЁЭЬГ = 16 × 180
⇒ ЁЭЬГ `=(16×180)/(0.8×22)`= 163.64°
Area of sector =`theta/360^@× pir^2 =163.64^@/360^@×22/7`× 5.6 × 5.6
=`163.64/180`× 11 × 0.8 × 5.6
= 44.8 cm2
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
The area of sector of circle of radius 2cm is ЁЭЬЛcm2. Find the angle contained by the sector.
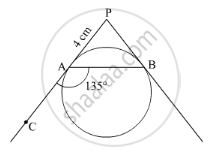
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
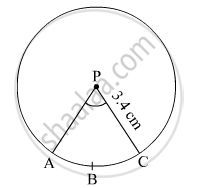
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
