Advertisements
Advertisements
प्रश्न
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
उत्तर
Let r be the radius of the circle.
Thus, we have ;
`r = 50/2 "m"`
= 25 m
Area left ungrazed = (Area of the square) - 4(Area of the sector where r = 25 m and θ = 90°)
`=|(50xx50)-4(3.14xx25xx25xx90/360)|"m"^2`
`=|2500-(4xx(19625)/4)|"m"^2`
`=(2500 - 1962.5) "m"^2`
= 537.5 m2
APPEARS IN
संबंधित प्रश्न
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
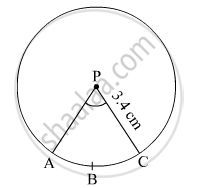
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.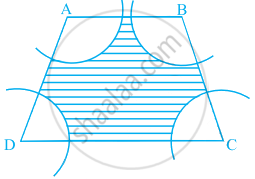
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
