Advertisements
Advertisements
प्रश्न
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
उत्तर
Given radius = r = `5sqrt(2)` cm = OA = OB
Length of chord AB = 10cm
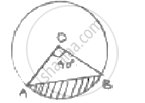
In ΔOAB, OA = OB =` 5sqrt(2)` 𝑐𝑚 AB = 10cm
`OA^2 + OB^2 = (5sqrt(2))^2+ (5sqrt(2))^2= 5 0 + 50 = 100 = (AB)^2`
Pythagoras theorem is satisfied OAB is right triangle
𝜃 = angle subtended by chord = ∠AOB = 90°
Area of segment (minor) = shaded region
= area of sector - area of `triangle`OAB
=`theta/360× pir^2 −1/2`× 𝑂𝐴 × 𝑂𝐵
=`90/360×22/7(5sqrt(2))^2−1/2× 5sqrt(2) × 5sqrt(2)`
=`275/7− 25 −100/7 cm^2`
Area of major segment = (area of circle) – (area of minor segment)
= `pir^2`2 −`100/7`
=`22/7× (5sqrt(2))^2−100/7`
=`1100/7−100/7`
=`1000/7 cm^2`
APPEARS IN
संबंधित प्रश्न
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.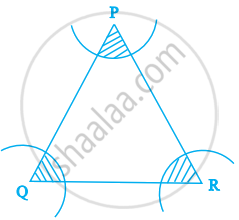
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
