Advertisements
Advertisements
Question
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
Solution
Given radius = r = `5sqrt(2)` cm = OA = OB
Length of chord AB = 10cm
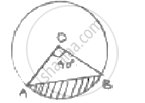
In ΔOAB, OA = OB =` 5sqrt(2)` 𝑐𝑚 AB = 10cm
`OA^2 + OB^2 = (5sqrt(2))^2+ (5sqrt(2))^2= 5 0 + 50 = 100 = (AB)^2`
Pythagoras theorem is satisfied OAB is right triangle
𝜃 = angle subtended by chord = ∠AOB = 90°
Area of segment (minor) = shaded region
= area of sector - area of `triangle`OAB
=`theta/360× pir^2 −1/2`× 𝑂𝐴 × 𝑂𝐵
=`90/360×22/7(5sqrt(2))^2−1/2× 5sqrt(2) × 5sqrt(2)`
=`275/7− 25 −100/7 cm^2`
Area of major segment = (area of circle) – (area of minor segment)
= `pir^2`2 −`100/7`
=`22/7× (5sqrt(2))^2−100/7`
=`1100/7−100/7`
=`1000/7 cm^2`
APPEARS IN
RELATED QUESTIONS
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
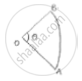
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?


Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Find the area of the unshaded region shown in the given figure.