Advertisements
Advertisements
Question
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
Solution
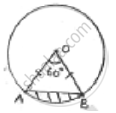
Given radius (r) = 14cm = OA = OB
𝜃 = angle at centre = 60°
In ΔAOB, ∠A = ∠B [angles opposite to equal sides OA and OB] = x
By angle sum property ∠A + ∠B + ∠O = 180°
x + x + 60° = 180° ⇒ 2x = 120° ⇒ x = 60°
All angles are 60°, OAB is equilateral OA = OB = AB
Area of segment = area of sector – area Δle OAB
=`theta/360^@× pir^2 − sqrt(3)/4× (−AB)^2`
=`60/360×22/7× 14 × 14 − sqrt(3)/4× 14 × 14`
=`308/3− 49sqrt(3)`
`= (308−147sqrt(3))/3cm^2`
APPEARS IN
RELATED QUESTIONS
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
Find the perimeter of a quadrant of a circle of radius 14 cm.
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
