Advertisements
Advertisements
Question
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
Solution
i . Perimeter of shaded region = Length of the arc APB + Length of the arc ARC + Length of the arc BSD + Length of the arc CQD
`=1/2xx2pi"r"_1 + 1/2xx2pi"r"_2 + 1/2xx2pi"r"_4`
`=1/2xx2pi(7/2) + 1/2xx2pi(7)+1/2xx2pi(7/2)`
`=2pi(7/2)+2pi(7)`
`=2pi(7/2+7)`
`=2xx22/7xx21/2`
= 66 cm
ii . Area of shaded region = Area of the arc ARC + Area of the arc BSD - (Area of the arc APB + Area of the arc CQD)
`=1/2xxpi("r"_1)^2+1/2xxpi("r")^2 - [1/2xxpi("r"_3)^2 + 1/2xxpi("r"_4)^2]`
`=1/2xxpi(7)^2+1/2xxpi(7)^2 - [1/2xxpi(7/2)^2+1/2xxpi(7/2)^2]`
`= pi(7)^2 - pi(7/2)^2`
`=pi(49 - 49/4)`
`=22/7xx147/4`
= 115.5 cm2
APPEARS IN
RELATED QUESTIONS
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
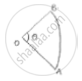
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
