Advertisements
Advertisements
Question
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
Solution
Let the radius of the sector AOBA be r.
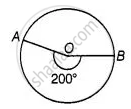
Given that, Central angle of sector AOBA = θ = 200°
And area of the sector AOBA = 770 cm2
We know that, area of the sector = `(pi"r"^2)/360^circ xx θ^circ`
∴ Area of the sector, 770 = `(pi"r"^2)/360^circ xx 200`
⇒ `(77 xx 18)/pi` = r2
⇒ r2 = `(77 xx 18)/22 xx 7`
⇒ r2 = 9 × 49
⇒ r = 3 × 7
∴ r = 21 cm
So, radius of the sector AOBA = 21 cm.
Now, the length of the corresponding arc of this sector = Central angle × Radius ...`[∵ θ = l/"r"]`
= `200 xx 21 xx pi/180^circ` ...`[∵ 1^circ = pi/180^circ "R"]`
= `20/18 xx 21 xx 22/7`
= `220/3 "cm"`
= `73 1/3 "cm"`
Hence, the required length of the corresponding arc is `73 1/3 "cm"`.
APPEARS IN
RELATED QUESTIONS
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
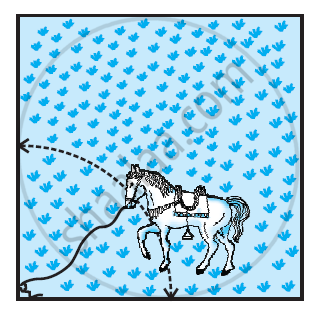
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).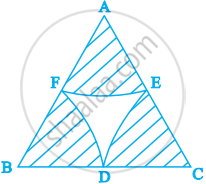
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
