Advertisements
Advertisements
Question
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
Solution
Length of arc of circle = 20 cm
Here, central angle θ = 60°
∴ Length of arc = `θ/360^circ xx 2π"r"`
⇒ 20 = `60^circ/360^circ xx 2π"r"`
⇒ `(20 xx 6)/(2π)` = r
∴ r = `60/π "cm"`
Hence, the radius of circle is `60/π`cm.
APPEARS IN
RELATED QUESTIONS
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
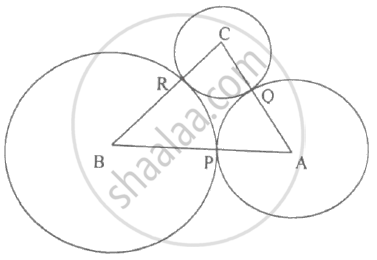
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
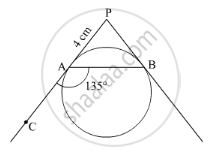
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?

(2) Area of any one of the sectors
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
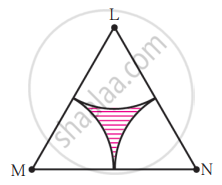
The area of the shaded portion in the following figure is equal to the area of.
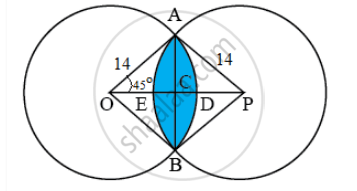
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
