Advertisements
Advertisements
Question
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
Solution
Given that, radius of the circle (r) = 21 cm and central angle of the sector AOBA (θ) = 120°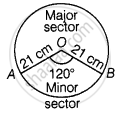
So, area of the circle
= πr2
= `22/7 xx (21)^2`
= `22/7 xx 21 xx 21`
= 22 × 3 × 21
= 1386 cm2
Now, area of the minor AOBA with central angle 120°
= `(pi"r"^2)/360^circ xx θ`
= `22/7 xx (21 xx 21)/360^circ xx 120`
= `(22 xx 3 xx 21)/3`
= 22 × 21
= 462 cm2
∴ Area of the major sector ABOA
= Area of the circle – Area of the sector AOBA
= 1386 – 462
= 924 cm2
∴ Difference of the areas of a sector AOBA and its corresponding major sector ABOA
= |Area of major sector ABOA – Area of minor sector AOBA|
= |924 – 462|
= 462 cm2
Hence, the required difference of two sectors is 462 cm2.
APPEARS IN
RELATED QUESTIONS
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

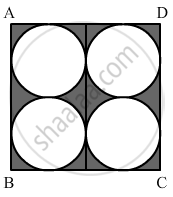
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
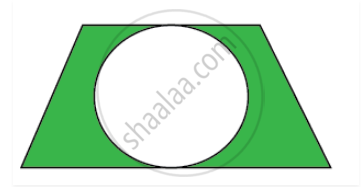
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
