Advertisements
Advertisements
Question
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

Solution
∠ AOB = q
Reflex ∠ AOB = 360 - q
Since arc AB subtends reflex ∠ AOB = (360 - q)° at the centre and ∠ ACB on the remaining part of the circle .
∴ ∠ ACB = `1/2` (reflex ∠ AOB)
If OACB is a parallelogram
∠ AOB = ∠ ACB
q = p
360 - 2p = p
3p = 360
p = 120°
APPEARS IN
RELATED QUESTIONS
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
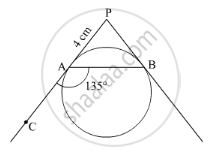
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
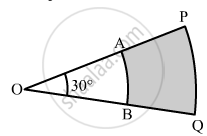
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.