Advertisements
Advertisements
Question
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
Solution
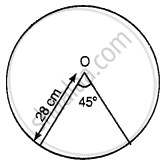
Given that, Radius of a circle, r = 28 cm
And measure of central angle θ = 45°
∴ Area of a sector of a circle = `(π"r"^2)/360^circ xx θ`
= `22/7 xx (28)^2/360^circ xx 45^circ`
= `(22 xx 28 xx 28)/7 xx 45^circ/360^circ`
= `22 xx 4 xx 28 xx 1/8`
= 22 × 14
= 308 cm2
Hence, the required area of a sector of a circle is 3082 cm.
APPEARS IN
RELATED QUESTIONS
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
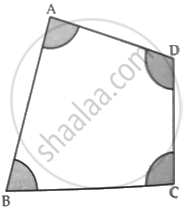
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
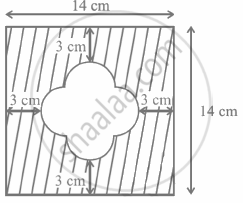
Find the area of the unshaded region shown in the given figure.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
