Advertisements
Advertisements
Question
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
Solution
Let a be the side of square.
∴ Diameter of a circle = Diagonal of the square = 8 cm
In right angled triangle ABC,
Using Pythagoras theorem,
(AC)2 = (AB)2 + (BC)2
∴ (8)2 = a2 + a2
64 = 2a2
a2 = 32
Hence,
Area of square = a2
= 32 cm2
∴ Radius of the circle = `"Diameter"/2`
∴ Area of the circle = πr2
= π(4)2
= 16 cm2
Therefore, the area of the shaded region = Area of circle – Area of square
The area of the shaded region = 16π – 32
= `16 xx (22/7) - 32`
= `128/7`
= 18.286 cm2
APPEARS IN
RELATED QUESTIONS
Find the area of the following circle, given that diameter = 49 m.
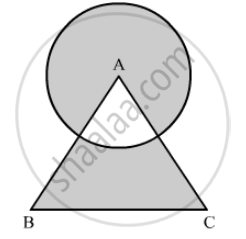
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
The area of the sector of angle θ° of a circle with radius R is
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
The radius of a circular wheel is 42 cm. Find the distance travelled by it in :
(i) 1 revolution ;
(ii) 50 revolutions ;
(iii) 200 revolutions ;
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
Pizza factory has come out with two kinds of pizzas. A square pizza of side 45 cm costs ₹ 150 and a circular pizza of diameter 50 cm costs ₹ 160 (Figure). Which pizza is a better deal?