Advertisements
Advertisements
प्रश्न
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
उत्तर
Let a be the side of square.
∴ Diameter of a circle = Diagonal of the square = 8 cm
In right angled triangle ABC,
Using Pythagoras theorem,
(AC)2 = (AB)2 + (BC)2
∴ (8)2 = a2 + a2
64 = 2a2
a2 = 32
Hence,
Area of square = a2
= 32 cm2
∴ Radius of the circle = `"Diameter"/2`
∴ Area of the circle = πr2
= π(4)2
= 16 cm2
Therefore, the area of the shaded region = Area of circle – Area of square
The area of the shaded region = 16π – 32
= `16 xx (22/7) - 32`
= `128/7`
= 18.286 cm2
APPEARS IN
संबंधित प्रश्न
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
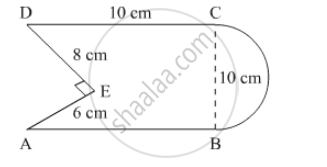
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
If diameter of a circle is increased by 40%, then its area increase by
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
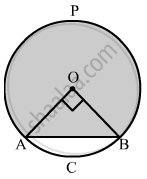
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
The minute hand of a clock is 12 cm long. Find the area swept by in it 35 minutes.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
