Advertisements
Advertisements
प्रश्न
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
उत्तर
Given that, radius of the circle (r) = 21 cm and central angle of the sector AOBA (θ) = 120°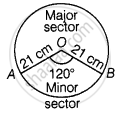
So, area of the circle
= πr2
= `22/7 xx (21)^2`
= `22/7 xx 21 xx 21`
= 22 × 3 × 21
= 1386 cm2
Now, area of the minor AOBA with central angle 120°
= `(pi"r"^2)/360^circ xx θ`
= `22/7 xx (21 xx 21)/360^circ xx 120`
= `(22 xx 3 xx 21)/3`
= 22 × 21
= 462 cm2
∴ Area of the major sector ABOA
= Area of the circle – Area of the sector AOBA
= 1386 – 462
= 924 cm2
∴ Difference of the areas of a sector AOBA and its corresponding major sector ABOA
= |Area of major sector ABOA – Area of minor sector AOBA|
= |924 – 462|
= 462 cm2
Hence, the required difference of two sectors is 462 cm2.
APPEARS IN
संबंधित प्रश्न
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
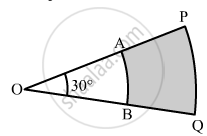
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
