Advertisements
Advertisements
प्रश्न
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
उत्तर
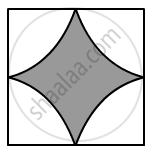
Each cow can graze a region that cannot be accessed by other cows.
∴ Radius of the region grazed by each cow `=50/2 = 25 "m"`
Area that each cow grazes`=1/4xxpixx"r"^2`
`= 1/4xx3.14xx25xx25`
= 490.625 cm2
Total area grazed = 4 × 490.625 = 1963.49 m2
Area of the square = (Side)2
= 502
= 2500 cm2
Now,
Area left ungrazed= Area of the square - Grazed area
= 2500 - 1963.49 = 536.51 m2
APPEARS IN
संबंधित प्रश्न
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
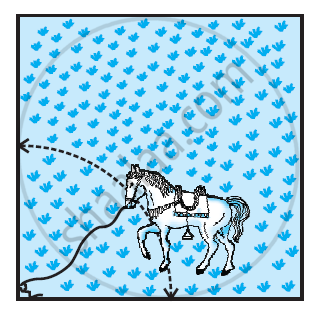
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
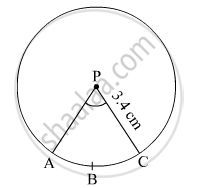
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
