Advertisements
Advertisements
प्रश्न
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
उत्तर
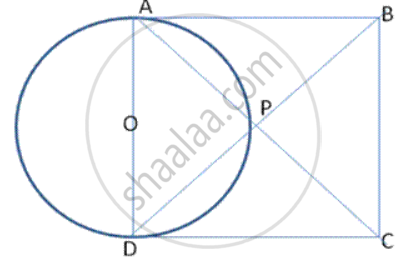
We know that the diagonals of a rhombus bisect each other at right angles.
∴ ∠ APO =90° - (1)
Also, AD is the diameter of the circle with centre 0
∴ ∠ APD=90° - (2) (Angle in semi circle)
From ( 1) and (2), we get, The cirde drawn with any side of a rhombus as a diameter, passes through point of intersection of its diagonals.
APPEARS IN
संबंधित प्रश्न
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Find the area of the unshaded region shown in the given figure.