Advertisements
Advertisements
प्रश्न
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
उत्तर १
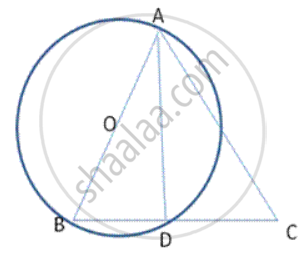
To prove: BD =DC
Proof: let .AB be the diameter of the circle with centre O
∴ ∠ ADB = 900 (Angles in a semicirde is a right triangle)
∠ ADB + ∠ ADC = 180 (linear pair)
∴ ∠ ADC = 180 - 90 = 90°
In Δ ADB and Δ ADC
AB= AC (given)
∠ ADB = ∠ ADC (90"each)
AD= AD (Common)
∴ Δ ADB ≅ Δ ADC (RHS)
Hence BD = DC (CPCT)
उत्तर २
Given: In Isosceles Δ ABC. A circle is drawn taken AB as diameter which intersects BC at D.
To prove : BD = DC
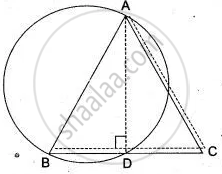
Construction: Join AD.
Proof: ∠ADB = 90° ...(Angle of semi-circle)
In Δ ABD and Δ ACD,
AB = AC ...(Given)
∠ADB = ∠ADC ...(90°)
AD = AD ....(Common)
∴ Δ ABD ≅ Δ ACD
Hence, BD = DC.
APPEARS IN
संबंधित प्रश्न
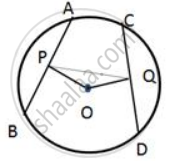
In the following figure; P and Q are the points of intersection of two circles with centres O and O’. If straight lines APB and CQD are parallel to O O'; prove that:
(i) O O' = `1/2AB` (ii) AB = CD
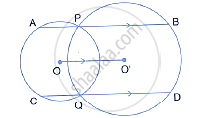
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O1 and O2 are the centers of two circles.

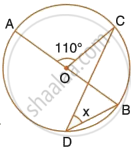
In the figure, given alongside, AOB is a diameter of the circle and ∠AOC = 110°. Find ∠BDC.
In the figure, chords AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE.
In the given figure, QAP is the tangent at point A and PBD is a straight line.
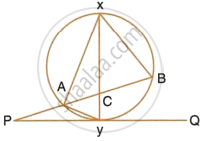
If ∠ACB = 36° and ∠APB = 42°, find:
- ∠BAP
- ∠ABD
- ∠QAD
- ∠BCD
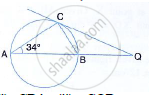
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.
If ∠CAB = 34°, Find : ∠CBA
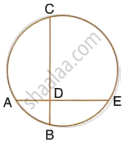
Prove that the line segment joining the midpoints of two parallel chords of a circle passes through its centre.
Two circles are drawn with sides AB, AC of a triangle ABC as diameters. They intersect at a point D. Prove that D lies on BC.
In following figure , chord ED is parallel to the diameter AC of the circle. Given ∠ CBE = 65° , calculate ∠DEC .
In the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.