Advertisements
Advertisements
प्रश्न
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
उत्तर
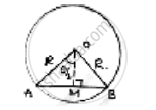
Let radius of circle = r
Area of circle = 𝜋𝑟2
AB is a chord, OA, OB are joined drop OM ⊥ AB. This OM bisects AB as well as ∠AOB.
∠AOM = ∠MOB =`1/2(0) =theta/2` AB = 2AM
In ΔAOM, ∠AMO = 90°
`"Sin"theta/2=(AM)/(AD)⇒ AM = R."sin"theta/2` AB = 2R sin`theta/2`
`"Cos"theta/2=(OM)/(AD)⇒ OM = R"cos"theta/2`
Area of segment cut off by AB = (area of sector) – (area of triangles)
=`theta/360× pir^2 −1/2`× 𝐴𝐵 × 𝑂𝑀
`= r^2 [(pitheta)/360^@−1/2. 2"rsin"theta/2. R" cos"theta/2]`
`= R^2 [(pitheta)/360^@− "sin"theta/2. "cos"theta/2]`
Area of segment =`1/2`(𝑎𝑟𝑒𝑎 𝑜𝑓 𝑐𝑖𝑟𝑐𝑙𝑒)
`r^2 [(pitheta)/360− "sin"theta/2." cos"theta/2] =1/8pir^2`
`(8pitheta)/360^@− 8 "sin"theta/2. "cos"theta/2= pi`
`8 "sin"theta/2. "cos"theta/2+ pi =(pitheta)/45`
APPEARS IN
संबंधित प्रश्न
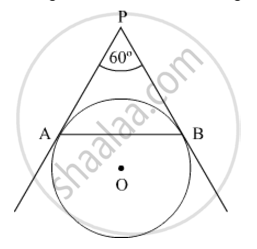
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

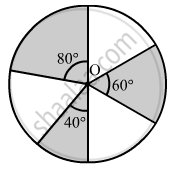
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
