Advertisements
Advertisements
प्रश्न
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
उत्तर
Let O be the centre of the circle and AB be the chord.
Consider Δ OAB.
OA = OB = `5sqrt(2) "cm"`
OA2 + OB = 50 + 50 = 100
Now,
`sqrt(100) = 10 "cm" = "AB"`
Thus, ΔOAB is a right isosceles triangle.
Thus we have :
Area of Δ OAB `=1/2xx5sqrt(2)xx5sqrt(2) = 25 "cm"^2`
Area of the minor segment = Area of the sector - Area of the triangle
`=(90/360xxpixx(5sqrt(2))^2) - 25`
= 14.25 cm2
Area of the major segment = Area of the circle -- Area of the minor segment
`= pixx(5sqrt(2))^2-14.25`
= 142.75 cm2
APPEARS IN
संबंधित प्रश्न
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
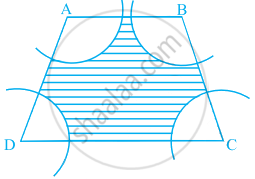
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.