Advertisements
Advertisements
प्रश्न
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
उत्तर

We know that in 1 hour (i.e., 60 minutes), the minute hand rotates 360°.
In 5 minutes, minute hand will rotate = `360^@/60xx5 = 30^@`
Therefore, the area swept by the minute hand in 5 minutes will be the area of a sector of 30° in a circle of 14 cm radius.
Area of sector of angle θ = `θ/(360°) xx pir^2`
Area of sector of 30° =`(30°)/(360°)xx22/7xx14xx14`
`=22/12xx2xx14`
`=(11xx14)/3`
=`154/3` cm2
Therefore, the area swept by the minute hand in 5 minutes is `154/3` cm2
APPEARS IN
संबंधित प्रश्न
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
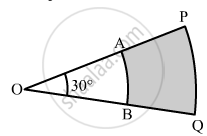
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
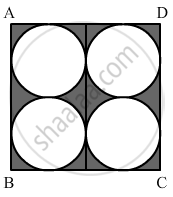
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.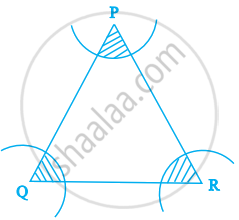
Find the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60° (Use π = 3.14).
