Advertisements
Advertisements
प्रश्न
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
उत्तर
Given that, radius of each arc (r) = 21 cm
Area of sector with ∠A
= `(∠"A")/360^circ xx π"r"^2`
= `(∠"A")/360^circ xx π xx (21)^2 "cm"^2`
Area of sector with ∠B
= `(∠"B")/360^circ xx π"r"^2`
= `(∠"B")/360^circ xx π xx (21)^2 "cm"^2`
Area of sector with ∠C
= `(∠"C")/360^circ xx π"r"^2`
= `(∠"C")/360^circ xx π xx (21)^2 "cm"^2`
And area of sector with ∠D
= `(∠"D")/360^circ xx π"r"^2`
= `(∠"D")/360^circ xx π xx (21)^2 "cm"^2`
Therefore, sum of the areas (in cm2) of the four sectors
= `(∠"A")/360^circ xx π xx (21)^2 + (∠"B")/360^circ xx π xx (21)^2 + (∠"C")/360^circ xx π xx (21)^2 + (∠"D")/360^circ xx π xx (21)^2`
= `π/360^circ xx (21)^2 xx [∠"A" + ∠"B" + ∠"C" + ∠"D"]`
= `π/360^circ xx (21)^2 xx 360^circ` ...[∵ Sum of all interior angles in a quadrilateral = 360°]
= `22/7 xx 21 xx 21`
= 22 × 3 × 21
= 1386
Hence, the required area of the shaded region is 1386 cm2.
APPEARS IN
संबंधित प्रश्न
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
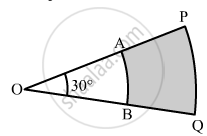
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
