Advertisements
Advertisements
प्रश्न
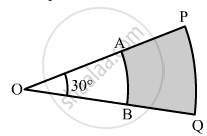
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
उत्तर
Area of the shaded portion = Area of sector OPQ − Area of sector OAB
`= 30^circ/360xxpi(7)^2 - 30^circ/360^circxxpi(3.5)^2`
`=22/7xx1/12[(7)^3 - (3.5)^2]`
`= 22/7 xx 1/12[(7)^2-(7/2)^2]`
`=22/7xx1/12xx147/4`
`=77/8 "cm"^2`
Hence, the area of the shaded portion is`77/8` cm2 .
APPEARS IN
संबंधित प्रश्न
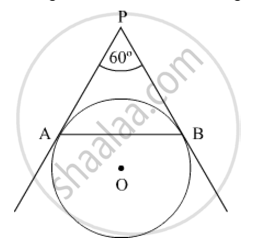
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
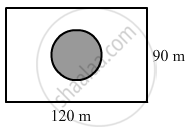
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).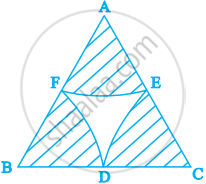
Find the perimeter of a quadrant of a circle of radius 14 cm.
