Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
A chord of a circle of radius 10 cm subtends a right angle at the centre of the circle. Find the area of the corresponding minor segment. [Use π = 3.14]
उत्तर १

Let AB be the chord of a circle subtending an angle of 90° at the centre O of the circle.
Area of sector = `theta/(360^circ) x pi^2`
`= (90^circ)/(360^circ) xx 314 /100 xx 10xx10` cm2
= `1/4 xx 314` cm2
`= 157/2` cm2
= 78.5 cm2
Corresponding minor segment = ΔAOB
= 78.5 cm2 − `[1/2 xx10 xx10]`
= 78.5 cm2 − 50 cm2
= 28.5 cm2
उत्तर २

Area of minor segment = Area of sector AOBC − Area of right triangle AOB
`=theta/360^circpi("OA")^2 - 1/2xx` OA× OB `
`= 90^circ/360^circxx3.14(10)^2 - 1/2xx10xx10`
= 78.5 − 50
= 28.5 cm2
Hence, the area of minor segment is 28.5 cm2
Notes
Students should refer to the answer according to their question and preferred marks.
APPEARS IN
संबंधित प्रश्न
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.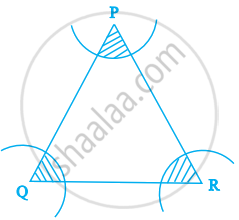
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
