Advertisements
Advertisements
प्रश्न
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
उत्तर
Let the radius of the sector AOBA be r.
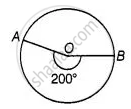
Given that, Central angle of sector AOBA = θ = 200°
And area of the sector AOBA = 770 cm2
We know that, area of the sector = `(pi"r"^2)/360^circ xx θ^circ`
∴ Area of the sector, 770 = `(pi"r"^2)/360^circ xx 200`
⇒ `(77 xx 18)/pi` = r2
⇒ r2 = `(77 xx 18)/22 xx 7`
⇒ r2 = 9 × 49
⇒ r = 3 × 7
∴ r = 21 cm
So, radius of the sector AOBA = 21 cm.
Now, the length of the corresponding arc of this sector = Central angle × Radius ...`[∵ θ = l/"r"]`
= `200 xx 21 xx pi/180^circ` ...`[∵ 1^circ = pi/180^circ "R"]`
= `20/18 xx 21 xx 22/7`
= `220/3 "cm"`
= `73 1/3 "cm"`
Hence, the required length of the corresponding arc is `73 1/3 "cm"`.
संबंधित प्रश्न
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

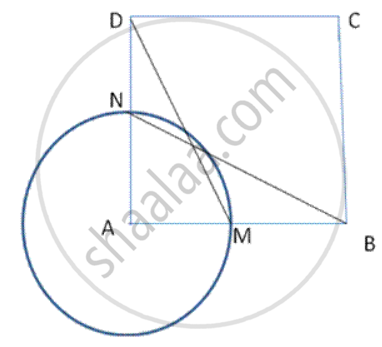
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
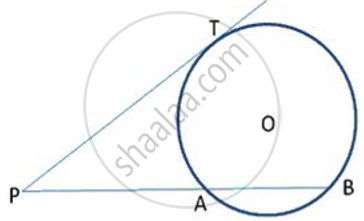
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
The area of the shaded portion in the following figure is equal to the area of.