Advertisements
Advertisements
प्रश्न
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
उत्तर

We know that in 1 hour (i.e., 60 minutes), the minute hand rotates 360°.
In 5 minutes, minute hand will rotate = `360^@/60xx5 = 30^@`
Therefore, the area swept by the minute hand in 5 minutes will be the area of a sector of 30° in a circle of 14 cm radius.
Area of sector of angle θ = `θ/(360°) xx pir^2`
Area of sector of 30° =`(30°)/(360°)xx22/7xx14xx14`
`=22/12xx2xx14`
`=(11xx14)/3`
=`154/3` cm2
Therefore, the area swept by the minute hand in 5 minutes is `154/3` cm2
APPEARS IN
संबंधित प्रश्न
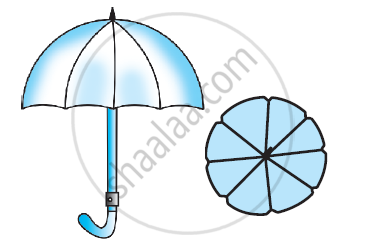
An umbrella has 8 ribs which are equally spaced. Assuming umbrella to be a flat circle of radius 45 cm. Find the area between the two consecutive ribs of the umbrella.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
(2) Area of any one of the sectors
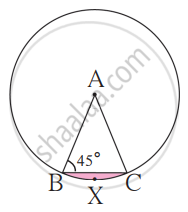
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
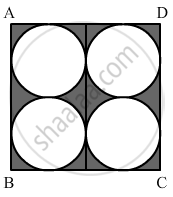
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
In figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle. Is the area of the outer square four times the area of the inner square? Give reasons for your answer.
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
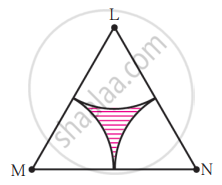
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
