Advertisements
Advertisements
प्रश्न
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
उत्तर
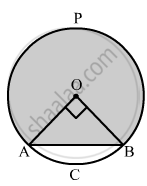
Area of minor segment = Area of sector AOBC − Area of right triangle AOB
`= (90°)/(360°) pi(OA)^2-1/2xx"OA"xx"OB"`
`=1/4xx22/7xx(7)^2-1/2xx7xx7`
`=1/4xx22/7xx(7)^2 - 1/2xx7xx7`
= 38.5 - 24.5
= 14 cm2
Area of major segment APB = Area of circle − Area of minor segment
`=(OA)^2 - 14`
`=22/7xx(7)^2-14`
= 154 - 14
= 140 cm2
Hence, the area of major segment is 140 cm2 .
APPEARS IN
संबंधित प्रश्न
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?


In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
Find the perimeter of a quadrant of a circle of radius 14 cm.
