Advertisements
Advertisements
प्रश्न

उत्तर
Radius of the circle, r = 7 cm
m(arc MBN) = ∠MON = θ = 60º
Area of the sector =` theta/360 xx pir^2`
⇒ Area ( O - MBN ) =`60/360 `× Area of circle
Area of the sector = \[\frac{\theta}{360º} \times \pi r^2 = \frac{60º}{360º } \times \frac{22}{7} \times \left( 7 \right)^2\] = 25.7 cm2
⇒ A(O- MBN) = 25.7 sq. cm
APPEARS IN
संबंधित प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
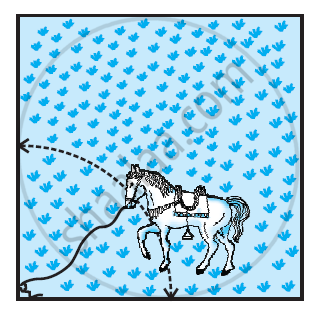
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
(2) Area of any one of the sectors
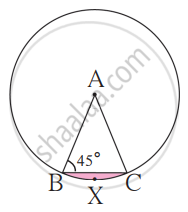
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
