Advertisements
Advertisements
प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
उत्तर
Radius (r) of circle = 21 cm
Angle subtended by the given arc = 60°
Length of an arc of a sector of angle θ = `theta/360^@xx2pir`

Length of arc ACB = `(60^@)/360^@ xx2xx22/7xx21`
`= 1/6xx2xx22xx3`
= 22 cm
Area of sector OACB = `(60^@)/(360^@)xxpir^2`
`= 1/6xx22/7xx21xx21`
= 231 cm2
In ΔOAB,
∠OAB = ∠OBA (As OA = OB)
∠OAB + ∠AOB + ∠OBA = 180°
2∠OAB + 60° = 180°
∠OAB = 60°
Therefore, ΔOAB is an equilateral triangle.
Area of ΔOAB = `sqrt3/4 xx ("Side")^2`
`= sqrt3/4 xx (21)^2 = (441sqrt3)/4 cm^2`
Area of segment ACB = Area of sector OACB − Area of ΔOAB
`= (231 - (441sqrt3)/4) cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
Find the area of a quadrant of a circle whose circumference is 22 cm. [Use `pi = 22/7`]
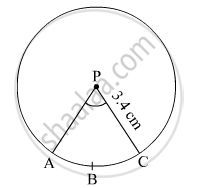
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

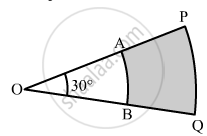
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
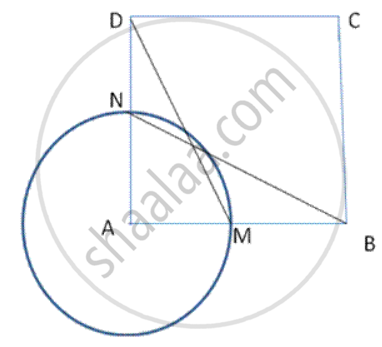
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.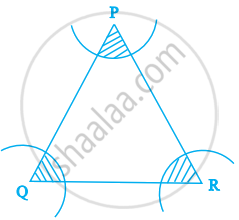
Find the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60° (Use π = 3.14).
