Advertisements
Advertisements
Question
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Solution
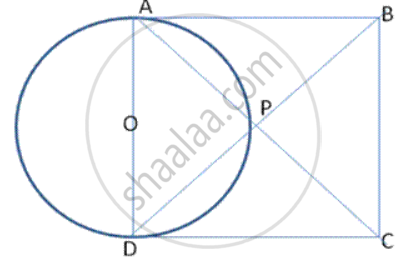
We know that the diagonals of a rhombus bisect each other at right angles.
∴ ∠ APO =90° - (1)
Also, AD is the diameter of the circle with centre 0
∴ ∠ APD=90° - (2) (Angle in semi circle)
From ( 1) and (2), we get, The cirde drawn with any side of a rhombus as a diameter, passes through point of intersection of its diagonals.
APPEARS IN
RELATED QUESTIONS
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
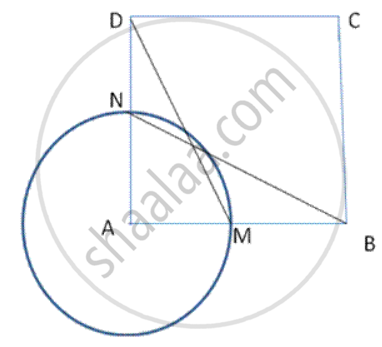
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
