Advertisements
Advertisements
Question
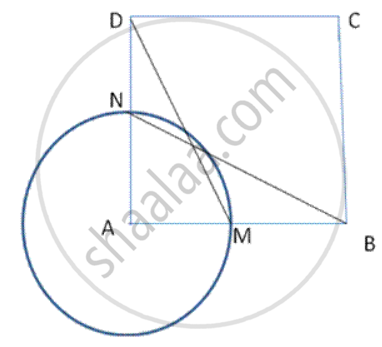
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Solution
In Δ DAM and Δ BAN
AN = AM (radii of same circle)
AD = AB (sides of square ABCD)
∠ DAM = ∠ BAN (common)
∴ Δ DAM ≅ Δ BAN.
APPEARS IN
RELATED QUESTIONS
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
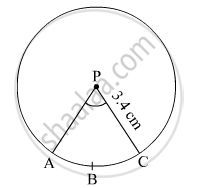
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
