Advertisements
Advertisements
Question
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
Solution
We know that the area A of a sector of an angle θ in the circle of radius r is given by `A=theta/360^@xxpi r^2`
It is given that r = 8 cm and θ = 135°.
Now we substitute the value of r and θ in above formula,
`A=135^@/360^@xxpixx8xx8 cm^2`
`=24 pi cm^2`
APPEARS IN
RELATED QUESTIONS
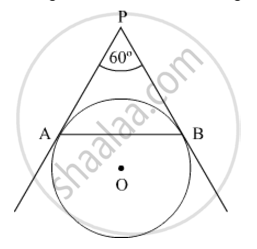
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`

Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
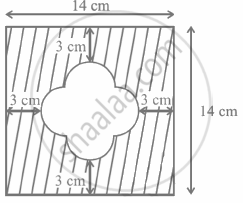
Find the area of the unshaded region shown in the given figure.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
