Advertisements
Advertisements
Question
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
Solution
Radius = 4 cm = r
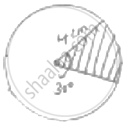
Angle subtended at centre = 𝜃 = 30°
Area of sector (shaded region)
=`theta/360^@× pir^2`
=`30/360×22/7`× 4 × 4
=`88/21cm^2`
∴ 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑟𝑒𝑞𝑢𝑖𝑟𝑒𝑑 𝑠𝑒𝑐𝑡𝑜𝑟 =`88/21cm^2`
APPEARS IN
RELATED QUESTIONS
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
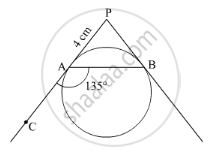
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?


The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
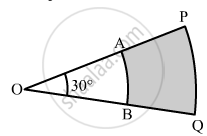
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).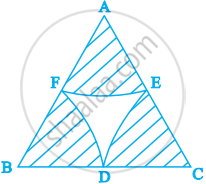
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
