Advertisements
Advertisements
Question
In fig, AB and CD are two equal chords of a circle with centre O. If M and N are the midpoints of AB and CD respectively,
prove that (a) ∠ ONM = ∠ ONM (b) ∠ AMN = ∠ CNM.
Solution

M and N are mid points of equal diords AB and CD respectively.
ON ⊥ CD and OM ⊥ AB
∴ ∠ ONC = ∠ OMA (90° each) ...(1)
(A line bisecting the chord and passing through the centre of the circle is perpendicular to the chord)
∴ AB = CD
ON = OM (equal chords are equidistant from the centre)
In Δ MON ,
MO = NO
∴ ∠ ONM = ∠ OMN ..(2)
Subtracting (2) from ( 1)
∠ONC - ∠ ONM = ∠ OMA - ∠ OMN
∠ CNM =∠ AMN
APPEARS IN
RELATED QUESTIONS
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
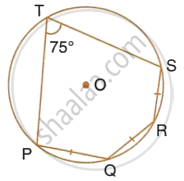
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
- ∠POS,
- ∠QOR,
- ∠PQR.
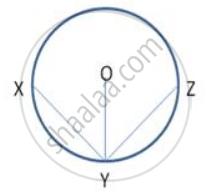
In following figure .,XY and YZ are two equal chords of a circle with centre O. Prove that the bisector of ∠ XYZ passes through O.
In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD.
In fig., chords AB and CD of a circle intersect at P. AP = 5cm, BP= 3cm and CP = 2.5cm. Determine the length of DP.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.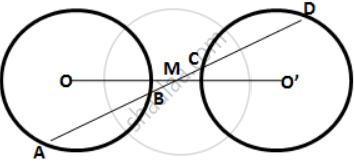
Prove that equal chords of congruent circles subtend equal angles at their center.
In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC, (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD
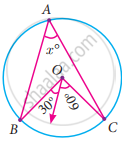
Find the value of x° in the following figure: