Advertisements
Advertisements
Question
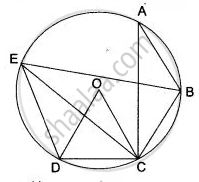
In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC, (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD
Solution
(i)
In Δ ABC,
∠ ABC + ∠ BAC + ∠ BCA = 180° ....( ∵ The sum of three angles of a triangle is 180°)
120° + ∠ BAC + ∠ BCA = 180° ....( ∵ ∠ ABC = 120° (Given))
∠ BAC + ∠ BCA = 60°
But, BA = BC.
∠ BAC + ∠ BCA = 60°
2 ∠ BCA = 60°
∠ BCA = 30°
(ii) ∠ BEC = ∠ BAC = 30°
(iii)
AB = BC = CD
Arc AB = Arc BC = Arc CD
Now,
∠ COB = 2 ∠ CAB
∠ COB = 2 x 30° = 60°
∠ DOC = ∠ COB = 60°
∠ DEC = `1/2 "∠ DOC" = 1/2 xx 60° = 30° `
∴ ∠ BED = ∠ BEC + ∠ DEC
∠ BED = ∠ BAC + ∠ DEC
∠ BED = 30° + 30° = 60°
(iv) ∠ COD = 60°
APPEARS IN
RELATED QUESTIONS
Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle, prove that:
(i) AP = CP,
(ii) BP = DP
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the area of the rhombus is `32sqrt(3) cm^2` find the radius of the circle.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
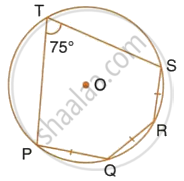
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
- ∠POS,
- ∠QOR,
- ∠PQR.
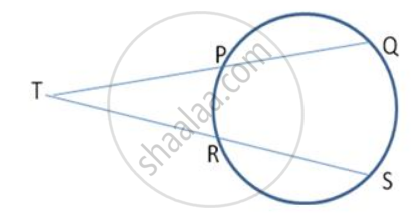
In fig. the centre of the circle is O. PQ and RS are two equal chords of the circle which , when produced , meet at T outside the circle . Prove that (a) TP = TR (b) TQ = TS.
Two congruent drdes have their centres at 0 and P. Mis the midpoint of the line segment OP. A straight line is drawn through M cutting the two circles at the points A, B, C and D. Prove that the chords AB and CD are equal.
AB and AC are two equal chords of a circle with centre o such that LABO and LCBO are equal. Prove that AB = BC.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.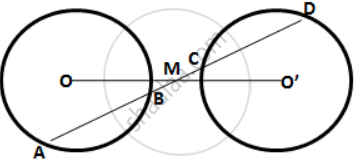
Prove that equal chords of congruent circles subtend equal angles at their center.
Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB
