Advertisements
Advertisements
प्रश्न
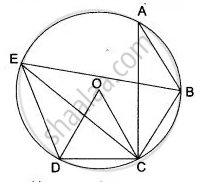
In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC, (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD
उत्तर
(i)
In Δ ABC,
∠ ABC + ∠ BAC + ∠ BCA = 180° ....( ∵ The sum of three angles of a triangle is 180°)
120° + ∠ BAC + ∠ BCA = 180° ....( ∵ ∠ ABC = 120° (Given))
∠ BAC + ∠ BCA = 60°
But, BA = BC.
∠ BAC + ∠ BCA = 60°
2 ∠ BCA = 60°
∠ BCA = 30°
(ii) ∠ BEC = ∠ BAC = 30°
(iii)
AB = BC = CD
Arc AB = Arc BC = Arc CD
Now,
∠ COB = 2 ∠ CAB
∠ COB = 2 x 30° = 60°
∠ DOC = ∠ COB = 60°
∠ DEC = `1/2 "∠ DOC" = 1/2 xx 60° = 30° `
∴ ∠ BED = ∠ BEC + ∠ DEC
∠ BED = ∠ BAC + ∠ DEC
∠ BED = 30° + 30° = 60°
(iv) ∠ COD = 60°
APPEARS IN
संबंधित प्रश्न
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
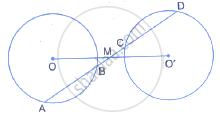
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
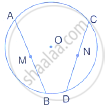
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN = ∠DNM.
(ii) ∠AMN = ∠CNM.
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
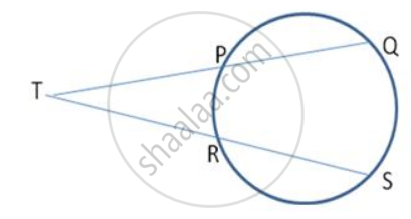
In fig. the centre of the circle is O. PQ and RS are two equal chords of the circle which , when produced , meet at T outside the circle . Prove that (a) TP = TR (b) TQ = TS.
Two congruent drdes have their centres at 0 and P. Mis the midpoint of the line segment OP. A straight line is drawn through M cutting the two circles at the points A, B, C and D. Prove that the chords AB and CD are equal.
In fig., chords AB and CD of a circle intersect at P. AP = 5cm, BP= 3cm and CP = 2.5cm. Determine the length of DP.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.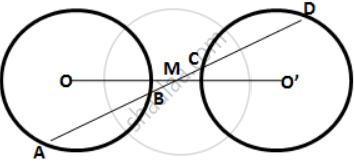
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP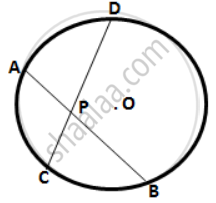
Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB
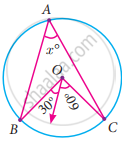
Find the value of x° in the following figure: