Advertisements
Advertisements
प्रश्न
In fig., chords AB and CD of a circle intersect at P. AP = 5cm, BP= 3cm and CP = 2.5cm. Determine the length of DP.
उत्तर
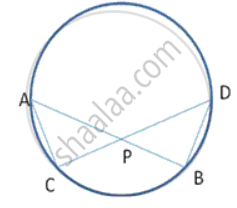
Let DP = x cm
In Δ APC and Δ DPB
∠ PAC = ∠ PDB (angles in the some segment)
∠ APC = ∠ DPB (vertically opposite angle)
∴ Δ APC ~ Δ DPB {AA corollary)
`"AP"/"DP" = "PC"/"PB"` (similar sides of similar triangles)
`5/"x" = 2.5/3`
`=> "x" = 15/2.5 = 150/25` = 6 cm
APPEARS IN
संबंधित प्रश्न
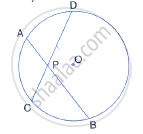
Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle, prove that:
(i) AP = CP,
(ii) BP = DP
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the area of the rhombus is `32sqrt(3) cm^2` find the radius of the circle.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
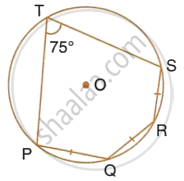
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
- ∠POS,
- ∠QOR,
- ∠PQR.
In fig. the centre of the circle is O. PQ and RS are two equal chords of the circle which , when produced , meet at T outside the circle . Prove that (a) TP = TR (b) TQ = TS.
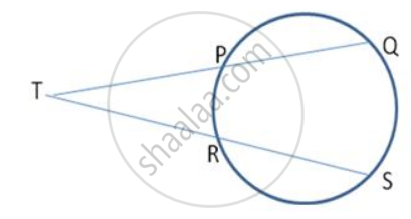
Two congruent drdes have their centres at 0 and P. Mis the midpoint of the line segment OP. A straight line is drawn through M cutting the two circles at the points A, B, C and D. Prove that the chords AB and CD are equal.
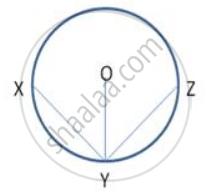
In following figure .,XY and YZ are two equal chords of a circle with centre O. Prove that the bisector of ∠ XYZ passes through O.
In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD.
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP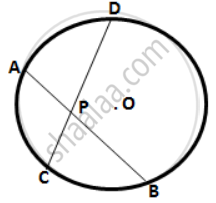
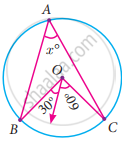
Find the value of x° in the following figure: