Advertisements
Advertisements
प्रश्न
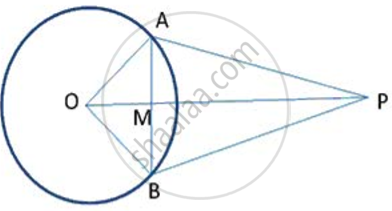
From a point P outside a circle, with centre O. tangents PA and PB are drawn as following fig., Prove that ∠ AOP = ∠ BOP and OP is the perpendicular bisector of AB.
उत्तर
In Δ AOP =Δ BOP
AP = PB (lengths of tangents drawn from and external point to a circle are equal)
OP = PO (common)
∠ PAO = ∠ PBO = 90 ° (radius is ⊥ to tangent at the point of contact)
∴ Δ AOP ≅ Δ BOP {By RHS}
Δ AOP = Δ BOP {By CPCT}
In Δ AMO and Δ BMO
AO = OB (radius of same circle)
∠ MOA = ∠ MOB {Proved above)
OM = MO {Common)
∴ Δ AMO ≅ Δ BMO {By CPCT}
∠ AMO = ∠ BMO
∠ AMO + ∠ BMO = 180°
∴ 2 ∠ AMO = 180°
∠ BMO = ∠ AMO = 90°
Hence, OP is the perpendicular bisector of AB.
APPEARS IN
संबंधित प्रश्न
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
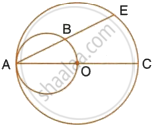
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
Two chords of lengths 10cm and 24cm are drawn parallel o each other in a circle. If they are on the same side of the centre and the distance between them is 17cm, find the radius of the circle.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the center.
AB and CD are two equal chords of a circle with center O which intersect each other at a right angle at point P.
If OM ⊥ AB and ON ⊥ CD;
show that OMPN is a square.
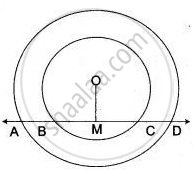
In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.
The radius of a circle is 13 cm and the length of one of its chord is 10 cm. Find the distance of the chord from the centre.
In Fig. O is the centre of the circle of radius 5 cm. OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 6 cm and CD = 8 cm. Determine PQ.

AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
