Advertisements
Advertisements
प्रश्न
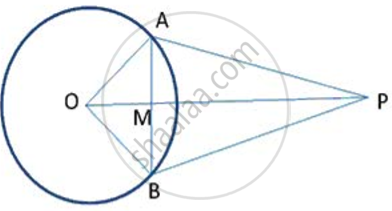
From a point P outside a circle, with centre O. tangents PA and PB are drawn as following fig., Prove that ∠ AOP = ∠ BOP and OP is the perpendicular bisector of AB.
उत्तर
In Δ AOP =Δ BOP
AP = PB (lengths of tangents drawn from and external point to a circle are equal)
OP = PO (common)
∠ PAO = ∠ PBO = 90 ° (radius is ⊥ to tangent at the point of contact)
∴ Δ AOP ≅ Δ BOP {By RHS}
Δ AOP = Δ BOP {By CPCT}
In Δ AMO and Δ BMO
AO = OB (radius of same circle)
∠ MOA = ∠ MOB {Proved above)
OM = MO {Common)
∴ Δ AMO ≅ Δ BMO {By CPCT}
∠ AMO = ∠ BMO
∠ AMO + ∠ BMO = 180°
∴ 2 ∠ AMO = 180°
∠ BMO = ∠ AMO = 90°
Hence, OP is the perpendicular bisector of AB.
APPEARS IN
संबंधित प्रश्न
AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the
radius of the circle is 13 cm. find the distance between the two chords.

A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of the circle.
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
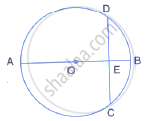
In Δ ABC, the perpendicular from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively. Prove that: arc CD = arc CE
A chord of length 8cm is drawn inside a circle of radius 6cm. Find the perpendicular distance of the chord from the centre of the circle.
A chord CD of a circle whose center is O is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm.
Calculate the lengths of: (i) CD ; (ii) AD ; (iii) CB.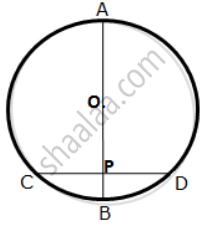
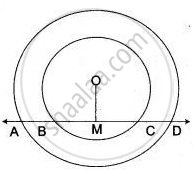
In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.
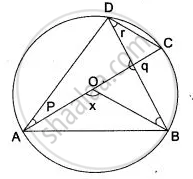
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
