Advertisements
Advertisements
प्रश्न
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
उत्तर
Let O be the centre of the circle OM and ON are perpendiculars on AB and CD.
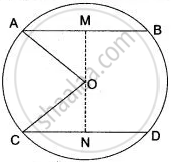
MON is one straight line.
Here
AM = `1/2`AB = 3 cm
CN = `1/2`CD = 4 cm
Let, ON = x cm and radius OA = OC = r cm
From right angled triangle OCN,
ON2 = OC2 - CN2 ...(By Pythagoras Theorem)
x2 = r2 - 16 ...(1)
From right-angled triangle OAM,
OM2 = OA2 - AM2 ...(By Pythagoras Theorem)
(7 - x)2 = r2 - 9 ...(2)
From (1) and (2),
(7 - x)2 - x2 = 7
49 + x2 - 14x - x2 = 7
14x = 42
x = 3
r2 = x2 + 16 ....(From(1))
r2 = 9 + 16 = 25
r = 5 cm
Hence, the radius of the circle is 5 cm.
APPEARS IN
संबंधित प्रश्न
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
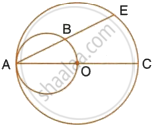
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC.
In the given figure, O is the centre of the circle with radius 5 cm. OP and OQ are perpendicular to AB and CD respectively. AB = 8 cm and CD = 6 cm. determine the length of PQ.
A chord CD of a circle whose center is O is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm.
Calculate the lengths of: (i) CD ; (ii) AD ; (iii) CB.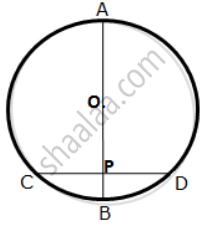
The radius of a circle is 17.0 cm and the length of the perpendicular drawn from its center to a chord is 8.0 cm.
Calculate the length of the chord.
In the following figure, AD is a straight line, OP ⊥ AD and O is the centre of both circles. If OA = 34cm, OB = 20 cm and OP = 16 cm;
find the length of AB.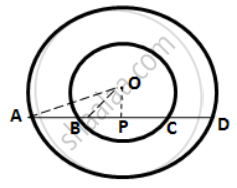
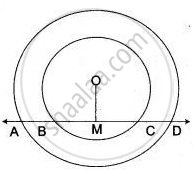
The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
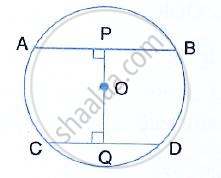
In the given figure, l is a line intersecting the two concentric circles, whose common center is O, at the points A, B, C, and D. Show that AB = CD.
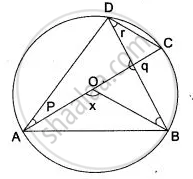
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.