Advertisements
Advertisements
प्रश्न
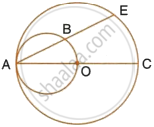
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
उत्तर
Join OB,
Then ∠OBA = 90°
(Angle in a semicircle is a right angle)
i.e. OB ⊥ AE
We know the perpendicular drawn from the centre to a chord bisects the chord.
Therefore, AB = BE
APPEARS IN
संबंधित प्रश्न
A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are
(i) on the opposite sides of the centre,
(ii) on the same side of the centre.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of
the circles. Show that:
(i) AB = CD,
(ii) AC = BD.

Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
The given figure shows two circles with centres A and B; and radii 5 cm and 3 cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

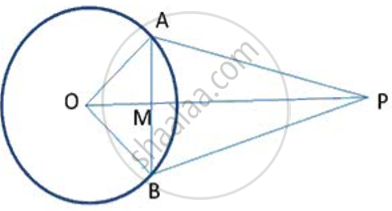
From a point P outside a circle, with centre O. tangents PA and PB are drawn as following fig., Prove that ∠ AOP = ∠ BOP and OP is the perpendicular bisector of AB.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords,
if both the chords are:
(i) on the opposite sides of the centre;
(ii) on the same side of the centre.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.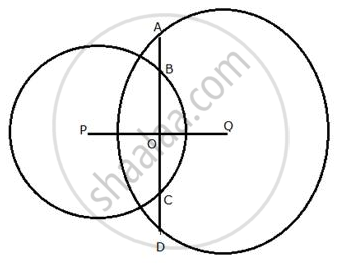
M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O.
Prove that: (i) ∠BMN = ∠DNM
(ii) ∠AMN = ∠CNM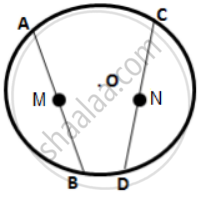
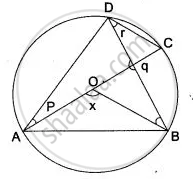
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.