Advertisements
Advertisements
प्रश्न
Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
उत्तर
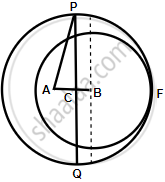
If two circles touch internally, then distance between their centres is equal to the difference of their radii.
So, AB = (5 − 3) cm = 2 cm.
Also, the common chord PQ is the perpendicular bisector of AB.
Therefore, AC = CB = `1/2` AB = 1 cm
In right ΔACP, we have AP2 = AC2 + CP2
`=>` 52 = 12 + CP2
`=>` CP2 = 25 – 1 = 24
`=> CP = sqrt(24)= 2 sqrt(6) cm`
Now, PQ = 2 CP
= `2 xx 2sqrt(6) cm`
= `4sqrt(6) cm`
APPEARS IN
संबंधित प्रश्न
AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the
radius of the circle is 13 cm. find the distance between the two chords.

A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its centre to a chord is 8.0 cm. Calculate the length of the chord.
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
A chord of length 8cm is drawn inside a circle of radius 6cm. Find the perpendicular distance of the chord from the centre of the circle.
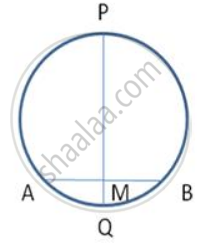
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
OP is the ⊥ bisector of chord AB.
The figure shows two concentric circles and AD is a chord of a larger circle.
Prove that: AB = CD.
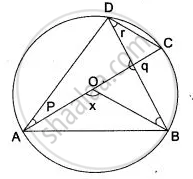
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
